Logarithmus
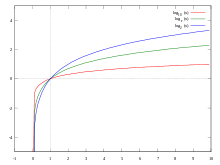
Linea rubra est logarithmus decimalis; linea caerulea, logarithmus binarius; linea viridis, logarithmus naturalis
Logarithmus est functio mathematica loga:R+∖{0}→R,x↦loga(x), (a∈R+∖{0}){displaystyle log _{a}:mathbb {R} ^{+}setminus lbrace 0rbrace to mathbb {R} ,xmapsto log _{a}(x), (ain mathbb {R} ^{+}setminus lbrace 0rbrace )}, cuius valor indicat exponentem variabilis independentis x ad basim a potentiae, id est: y=loga(x)⇔ay=x.{displaystyle y=log _{a}(x)Leftrightarrow a^{y}=x.}
Exempla:
log10(10) = 1 quia 101 = 10
log10(100) = 2 quia 102 = 100
log10(1000) = 3 quia 103 = 1000
- logarithmus decimalis seu vulgaris[1]: logarithmus pro basi 10
- log10(1000) lege: logarithmus decimalis quantitatis mille
- logarithmus naturalis seu hyperbolicus[2]: logarithmus pro basi e (Numero Euleri).
- Nota: Basis in formulis saepe omittitur; itaque logarithmus decimalis scribitur lg aut log, logarithmus naturalis ln.
Index
1 Arithmetica et logarithmi
2 Usus logarithmorum
3 Definitio et proprietates functionis
4 Historia logarithmorum
5 Notae
6 Bibliographia
7 Nexus externi
Arithmetica et logarithmi |
Logarithmis possumus multiplicationem in additionem convertere, hoc modo. Si debemus multiplicare A et B, pone X = productum, hoc est AB = X. Tunc log(AB) = log(X) (secundum quemlibet basin). Sed log(AB) = log(A) + log(B). Ergo si logarithmos addimus, possumus logarithmum producti scire, tunc productum ipsum. Exemplum:
- 1234∗7654=X{displaystyle 1234*7654=X}
- ln(1234)≈7.1180162045{displaystyle ln(1234)approx 7.1180162045}
- ln(7654)≈8.9429836660{displaystyle ln(7654)approx 8.9429836660}
- ln(1234)+ln(7654)≈16.0609998705{displaystyle ln(1234)+ln(7654)approx 16.0609998705}
- et 16.0609998705 est ln(9445036.0004629891)
- ergo 1234∗7654≈9445036{displaystyle 1234*7654approx 9445036} quod est re vera productum horum numerorum
Quare est log(AB) = log(A) + log(B)? Si X = log(A), secundum basin b, et Y = log(B) secundum eandem basin, tunc bX=A,bY=B{displaystyle b^{X}=A,b^{Y}=B} (per definitionem). Nunc AB=bXbY{displaystyle AB=b^{X}b^{Y}}, sed bXbY=bX+Y{displaystyle b^{X}b^{Y}=b^{X+Y}}. (Facilius est intellectu si X et Y sunt numeri integri; calculus nobis dicit id verum esse etiam si sint alii numeri reales.) Et logb(bX+Y)=X+Y{displaystyle log _{b}(b^{X+Y})=X+Y}, per definitionem. Habemus igitur logb(AB)=logb(A)+logb(B){displaystyle log _{b}(AB)=log _{b}(A)+log _{b}(B)}.

Regula remissaria ordinaria in usu discipulorum
Regula remissaria hac ratione utitur. In linea numerorum spatium inter numeros differentiam repraesentat: quod 5 - 2 = 6 - 3, spatium de puncto "2" ad punctum "5" idem est atque spatium inter puncta "3" et "6": est tres pedes. In regula remissaria, spatium rationem numerorum repraesantat: quod 6/2 = 3/1, spatium de punctum "2" ad punctum "6" idem est atque spatium inter puncta "3" et "1." Est ergo scala logarithmica.

Multiplicatio: 2×3=6{displaystyle 2times 3=6}
Regula duas scalas habet. Ut 2 per 3 multiplices, mitte "1" in scala superiore prope "2" in scala inferiore. Tunc "3" in scala superiore erit iuxta "6" in scala inferiore: spatium de "1" ad "3" in superiore scala idem est atque spatium de "2" ad "6" in inferiore. Et spatium non est 3 pedes, sed log(3) pedes.
Usus logarithmorum |

Scalae. Linea rubra est functio f(x)=10x{displaystyle f(x)=10^{x}}, linea viridis est f(x)=x{displaystyle f(x)=x}, linea caerula est f(x)=log(x){displaystyle f(x)=log(x)}. Prima chartula duas scalas lineares habet. In altera, scala valorum x est logarithmica, scala valorum y est linearis. In tertia, scala valorum x est linearis, alia logarithmica. In quarta ambo sunt scalae logarithmicae. Ut videtur, charta functionis logarithmicae est linea in secunda chartula, et charta functionis exponentialis in tertia.
Sunt quantitates in natura quae secundum regulam exponentialem variant, ut Potentia Hydrogenii in chemia, magnitudo terrae motus per scalam Richterianam descripta, magnitudo apparens stellarum in astronomia, Bit in informatica. Omnes secundum scalam logarithmicam calculantur. Talis scala utilis est cum valor mensurandus secundum rationem exponentialem auget.
Exempli gratia, si substantia quaedam habet potentiam hydrogenii (pH) 6 et alia habet pH 7, secunda decies plus protona habet quam prima.
Terrae motus magnitudine 5 fere decies maior est quam terrae motus magnitude 4, et fere decies rarior.
Definitio et proprietates functionis |
Ut supra dicitur, functio f(x)=loga(x){displaystyle f(x)=log _{a}(x)} est inversa functionis f(x)=ax{displaystyle f(x)=a^{x}}. Quod f(x)=ax{displaystyle f(x)=a^{x}} est functio continua, inversa f(x)=loga(x){displaystyle f(x)=log _{a}(x)} quoque est continua.
Possumus etiam logarithmum naturalem definire per integrale:[3]
- ln(x)=∫1x1tdt{displaystyle ln(x)=int _{1}^{x}{frac {1}{t}}dt}
si x > 0, ex qua formula scimus ddxln(x)=1x{displaystyle {frac {d}{dx}}ln(x)={frac {1}{x}}}, et functio ln(x) est continua. Cum x ad infinitatem tendet, ln(x) quoque sine fine auget. Et ln(1) = 0. Si 0 < x < 1, ln(x) < 0:
- ln(x)=∫1x1tdt{displaystyle ln(x)=int _{1}^{x}{frac {1}{t}}dt}
- Pone u=1t{displaystyle u={frac {1}{t}}} -- tunc
- ln(x)=∫11x−1udu=−∫11u1udu=−ln(1x){displaystyle ln(x)=int _{1}^{frac {1}{x}}{frac {-1}{u}}du=-int _{1}^{frac {1}{u}}{frac {1}{u}}du=-ln left({frac {1}{x}}right)}
Ergo limx→0ln(x)=−∞{displaystyle lim _{xto 0}ln(x)=-infty }
Si definitio per integrale re vera eandem functionem definit atque definitio per functionem inversam, debemus demonstrare ln(xy) = ln(x) + ln(y):
- ln(xy)=∫1xy1tdt{displaystyle ln(xy)=int _{1}^{xy}{frac {1}{t}}dt}
- Sit t = uy; tunc ln(xy)=∫1y1udu{displaystyle ln(xy)=int _{frac {1}{y}}{frac {1}{u}}du}
- quod est =∫1x1udu−∫11y1udu{displaystyle =int _{1}^{x}{frac {1}{u}}du-int _{1}^{frac {1}{y}}{frac {1}{u}}du}
- =ln(x)−ln(1y)=ln(x)+ln(y){displaystyle =ln(x)-ln left({frac {1}{y}}right)=ln(x)+ln(y)}
Functio hoc modo definita ergo easdem proprietates habet atque inversa functionis exponentialis: eadem est functio.
Numerus Euleri e est numerus cuius logarithmus naturalis est 1: ∫1e1tdt=1{displaystyle int _{1}^{e}{frac {1}{t}}dt=1}. Definitio functionis exponentialis y = ex est inversa functionis logarithmicae.
Si hoc modo logarithmum naturalem definimus, quo modo possumus logarithmos ad alias bases calculare? Sit loga(x)=ln(x)/ln(a){displaystyle log _{a}(x)=ln(x)/ln(a)}. Tunc:
- loga(x)=ln(x)ln(a){displaystyle log _{a}(x)={frac {ln(x)}{ln(a)}}}
- loga(x)×ln(a)=ln(x){displaystyle log _{a}(x)times ln(a)=ln(x)}
- eloga(x)ln(a)=eln(x)=x{displaystyle e^{log _{a}(x)ln(a)}=e^{ln(x)}=x}
- eln(a)loga(x)=aloga(x){displaystyle e^{{ln(a)}^{log _{a}(x)}}=a^{log _{a}(x)}}
- hoc est, x=a(loga(x){displaystyle x=a^{(log _{a}(x)}} ut desideremus.
Historia logarithmorum |

Frons libri Mirifici logarithmorum canonis descriptio ab Ioanne Napier anno 1614 editi.
Ioannes Napier, baro Murchiston, logarithmum primum describit, in libro anno 1614 edito, cuius titulus est Mirifici logarithmorum canonis descriptio.[4] Nomen logarithmus finxit e verbis Graecis λόγος (logos vel ratio) et ἀριθμός (arithmos vel numerus). Tabulas logarithmorum fecit ut facilius producta et rationes computaret.
Henricus Briggs, eius collega et professor geometriae in Universitate Oxoniensis, anno 1617 tabulas meliores fecit; qui librum edidit Logarithmorum chilias prima, in quo fuerunt logarithmi omnium numerorum integrorum de 1 ad 1000. Anno 1624 librum cuius titulus est Arithmetica logarithmica edidit, ubi logarithmos numerorum de 1 ad 10 000 et de 90 000 ad 100 000 calculavit.
Logarithmus secundum Napier non idem fuit atque logarithmus hodiernus; Briggs autem definitionem hodiernam habuit, secundum basin 10. Napier scivit summam exponentium cum numerorum producto cohaerere: si vis multiplicare bx et by, non opus est multiplicationi, quod productum est bx+y. Napier, si poterat basin b invenire ut omnes numerus N sit bx, multiplicare per additionem poterat. Et facilius esset si indices x essent parvi numeri, proximi inter se. Elegit ergo basin b = 0.9999999 = 1 - 10-7, sed nunc indices (exponentes) nimis proximae inter se fuerunt. Napier igitur omnia per 107 multiplicavit. Sit Nap(x) functio eius: tunc Nap(x) non re vera est log0.9999999(x){displaystyle log _{0.9999999}(x)}. Si x=107(1−1107)L{displaystyle x=10^{7}left(1-{frac {1}{10^{7}}}right)^{L}} (hoc est, bL × 107), Nap(x) = L. Ut faciliter videtur, Nap(107) = 0, et Nap(107(1−1107))=1{displaystyle Napleft(10^{7}left(1-{frac {1}{10^{7}}}right)right)=1}.
Multiplicatio ergo additio fit: Nap(a)+Nap(b)=Nap(ab107){displaystyle Nap(a)+Nap(b)=Napleft({frac {ab}{10^{7}}}right)}. Non exacte idem regulus est atque regulus logarithmorum verorum, quod necesse est punctum decimale movere post additionem, id quod autem perfacile est.
Quod limn→∞(1−1n)n=1e{displaystyle lim _{nrightarrow infty }left(1-{frac {1}{n}}right)^{n}={frac {1}{e}}}, functio Nap(x) similis est functioni log1e(x){displaystyle log _{frac {1}{e}}(x)}.
Briggs autem illum numerum 107 e regulo eicere voluit. Functionem similem Nap(x) definit, dicamus Br(x), ut Br(1) = 0, Br(10) = 1; tunc Br(√10) = .5 etc. Functio Br(x) est logarithmus decimalis.
Eodem fere tempore, Iobst Bürgi mathematicus Helveticus principia logarithmorum invenit, sed nihil ante anno 1620 edidit.
Notae |
↑ Eulerus, Leonhardus (1748). Introductio in analysin infinitorum, liber secundus, caput XXII, no. 529: "π... cujus numeri Logarithmus decimalis seu vulgaris est 0,497149872694133854351268288"
↑ Eulerus, Leonhardus (1748). Introductio in analysin infinitorum, liber primus, caput VII, no. 122: "2,71828182845904523536028... Quodsi iam ex hac basi logarithmi construantur, ii vocari solent logarithmi naturales seu hyperbolici, quoniam quadratura hyperbolae per istiusmodi logarithmos exprimi potest."
↑ Vide Hardy, p. 399-412
↑ Vide Boyer, p. 342 sqq., et Anglin et Lambek, p. 139–-143.
Bibliographia |
- Aigner, Martin, et Günter M. Ziegler. 2001. Proofs from THE BOOK, editio altera. Berolini: Springer. ISBN 3540678654
- Anglin, W. S., et J. Lambek. 1995. The Heritage of Thales. Berolini et Novi Eboraci: Springer. ISBN 038794544X.
- Bourbaki, Nicolas. 1976. Fonctions d'une variable réelle, editio nova, 2007. Berolini et Novi Eboraci: Springer. ISBN 978-3-540-34036-2.
- Boyer, Carl B. 1968. A History of Mathematics. Novi Eboraci: John Wiley & Sons. ISBN 0471093742.
- Bridger, Mark. 2007. Real Analysis: A Constructive Approach. Hoboken: Wiley Interscience. ISBN 9780471792307.
- Hardy, G. H. 1952. A Course in Pure Mathematics, ed. 10 (1992). Cantabrigiae. ISBN 0521092272.
- Krantz, Steven G. 2005. Real Analysis and Foundations. Boca Raton: Chapman & Hall. ISBN 1584884835.
- Rudin, Walter. 1974. Real and Complex Analysis, editio altera. Novi Eboraci: McGraw-Hill. ISBN 0-07-054233-3.
Nexus externi |
Powered by Google Text & Tabellen apud docs.google.com Arithmetica Logarithmica .mw-parser-output .existinglinksgray a,.mw-parser-output .existinglinksgray a:visited{color:gray}.mw-parser-output .existinglinksgray a.new{color:#ba0000}.mw-parser-output .existinglinksgray a.new:visited{color:#a55858}
(Anglice, Latine)
Logarithmi apud Wolfram MathWorld
(Anglice)
Logarithmi apud PurpleMath
(Anglice)
Logarithme -- approche, historique, définitions
(Francogallice)
Logarithmen und Logarithmusgesitze apud Mathematik.net
(Theodisce)







































