Htydjtk

Integrale functionis est una ex his duabus notionibus mathematicis:

• 
  functio quae est derivativum functionis datae (integrale indefinitum);


• numerus qui totum effectum functionis in certo intevallo describit (integrale definitum). Exemplum est magnitudo spatii inter lineam quae functionem repraesentat, x-axin et limites intervalli.

Theorema fundamentale calculi relationem inter has duas notiones indicat. Methodus integrale alicuius functionis inveniendi integratio vel calculus integralis (seu calculus summatorius (ſummatorius)^[1]) appellatur.

Integrale indefinitum |

Sit f{displaystyle f} functio in R{displaystyle mathbb {R} }. g(x)=∫f(x)dx{displaystyle g(x)=int f(x)dx} est integrale functionis f{displaystyle f} si dg(x)dx|x=y=f(y){displaystyle left.{frac {dg(x)}{dx}}right|_{x=y}=f(y)}.
Ex hac definitione sequitur etiam g(x)+C{displaystyle g(x)+C}, designante C{displaystyle C} quemcumque numerum realem, integrale functionis f{displaystyle f} esse. Quia C{displaystyle C} est quantitas constans, hoc est dCdx=0{displaystyle {frac {dC}{dx}}=0}, hic terminus nihil addit integrali.

Exempli gratia, si f(x)=x2{displaystyle f(x)=x^{2}}, tum ∫f(x)dx=x33+C{displaystyle int f(x)dx={frac {x^{3}}{3}}+C}.

Integrale definitum |

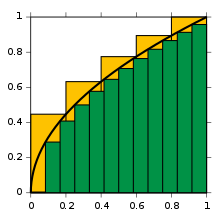
Approximatio integralis f(x) = √x inter 0 et 1

Integrale definitum ∫abf(x)dx{displaystyle int _{a}^{b}f(x)dx} est quasi summa collationum functionis f{displaystyle f} in omnibus punctis intervalli [a,b]{displaystyle [a,b]}.
Geometrice, integrale est magnitudo spatii inter lineam quae functionem repraesentat, x-axin et lineas x=a{displaystyle x=a} et x=b{displaystyle x=b}, si functio f{displaystyle f} est positiva in hoc intervallo. Si autem est negativa, ea magnitudo quoque negativa esse intellegitur.
Ad integrale definitum computandum, numerum infinitum functionis collationum infinitesimalium (hoc est omnibus numeris positivis inferior) addere opportet, quod per limitem definitur.

Exemplum hoc illustrabit. In adumbratione vides ∫01xdx{displaystyle int _{0}^{1}{sqrt {x}}dx}. Possumus magnitudinem aestimare si parva rectangula facimus, eisdem latitudinibus, altitudinibus autem f(xi){displaystyle f(x_{i})}, valores functionis in sinistris aut dextris lateribus intervallorum.

Talia rectangula in adumbratione reperiuntur. Sunt quinque rectangula, colore flavi, quorum latitudo est 1/5, et altitudines sunt √ 1/5, √ 2/5, √ 3/5, √ 4/5, et √ 1. Magnitudines rectangulorum igitur sunt (1/5) x √ 1/5, (1/5) x √ 2/5, et cetera; summatio earum magnitudinum est (fere) 0.74974.

Sunt etiam duodecim rectangula, colore viridi, quorum latitudo est 1/12 et altitudines sunt √ 0, √ 1/12, et cetera. Si magnitudines horum rectangulorum addimus, habemus (fere) 0.62029.

Integrale (per definitionem) est limes magnitudinum talium rectangulorum. Hoc est: Sit P={a0,a1,...an}{displaystyle P={a_{0},a_{1},...a_{n}}} copia numerorum inter a=a0{displaystyle a=a_{0}} et b=an{displaystyle b=a_{n}}, sicut ai<ai+1{displaystyle a_{i}<a_{i+1}}. Deinde summatio Riemanni est

∑i=1n(ai−ai−1)f(ai){displaystyle sum _{i=1}^{n}(a_{i}-a_{i-1})f(a_{i})}

et integrale est limes huius summationis dum n{displaystyle n} ad infinitatem it (aut, dum semper plures rectanguli sunt).^[2]Bernardus Riemann hanc definitionem invenit.

Saepe autem facilius est integrale alio modo computare. Theorema fundamentale calculi enim dicit:

∫abf(x)dx=F(b)−F(a){displaystyle int _{a}^{b}f(x)dx=F(b)-F(a)}, si dF(x)dx|x=y=f(y){displaystyle left.{frac {dF(x)}{dx}}right|_{x=y}=f(y)}

Ita integrale definitum computari potest si integrale indefinitum cognoscitur.

Usus |

• In physica, velocitas est derivativum loci, et acceleratio est derivativum velocitatis. Ergo, quia secundum Leges motus Newtoni acceleratio et vis, quae est quasi fundementum mechanicae, aequabiles sunt, locus alicuius rei ex viribus bis integrando computari potest.


• 
  Massa alicuius rei est integrale densitatis eius.


• In theoria probabilitatum probabilitas variabilis continui ex densitate probabilistica integrando computatur.

Notae |

Bibliographia |

• D. Bougainville 1764 Calculi infinitesimalis pars II., seu calculus integralis
  


• M. Hirsch 1823 Integral tables or collection of integral formulas
  


• 
  Leonhardus Eulerus 1827 Institutionum calculi integralis. Petropoli: impensis Academiae Imperialis Scientiarum. Volumen Primum Volumen Secundum Volumen Tertium Volumen Quartum
  


• Ferdinandus Minding 1849 Sammlung von Integraltafeln
  


• Davidus Bierens de Haan 1867 "Nouvelles Tables d'Intégrales définies." Leiden: P. Engels Volumen Primum Volumen Secudum
  


• Hardy, G. H. 1952 A Course of Pure Mathematics. Editio 10a. Cantabrigiae.


• Spivak, Michael. 1994 Calculus. Editio 3a. Houstoniae: Publish or Perish.