Theoria copiarum
Theoria copiarum est pars mathematicae in qua copiae tractantur, quae rerum collationes intelleguntur. Quamquam quaelibet res in copias colligi possunt, theoria copiarum plerumque rebus mathematicis adhibetur.

Georgius Cantor, anno 1894
Copiarum theoria nostrae aetatis a Georgio Cantor et Ricardo Dedekind annis 1870 inchoata est. Post theoriam paradoxorum in simplici copiarum theoria excogitatam multa systemata axiomatica saeculo vicesimo ineunte proposita sunt, quorum notissima sunt axiomata Zermelo-Fraenkel et axioma electionis.
Adhibentur vocabula copiarum theoriae ad omnes fere res mathematicas definiendas, sicut functiones, quin etiam notiones theoriae copiarum per totum curriculum mathematicae docendae inveniuntur. Principia copiarum et membrorum earum facile doceri possunt in schola primaria ope diagrammatum Venn et Euler, cum collectiones corporearum rerum cottidianarum discuntur. Qua in re etiam operationes facillimae, sicut unio intersectioque copiarum, exponi possunt. Notiones difficiliores, sicut cardinalitas, nulli curriculo baccalaureati quod quidem ad mathematicam artem attinet desunt.
Index
1 Definitiones
1.1 Elementa
1.2 Operationes
2 Axiomata et problemata
3 Disciplina theoriae
3.1 Exemplaria interiora
3.2 Modus coercens
3.3 Cardinales permagni
4 Historia
5 Nexus interni
6 Notae
7 Bibliographia
8 Nexus externi
Definitiones |
Imprimis definitiones ponendae quibus mathematici cottidie utuntur. Haec est simplex copiarum theoria, quam necesse erit subtiliorem facere.[1]
Elementa |
Cum copia sit conlatio rerum, hae res sunt elementa copiae. Si S={a,b,c,...}{displaystyle S={a,b,c,...}} est copia, dicimus "a est elementum copiae S," et scribimus a∈S{displaystyle ain S}. Est copia vacua vel inanis, quae nulla elementa habet; signum huius copiae est ∅{displaystyle emptyset }. Elementa copiae possunt quaelibet res esse, etiam aliae copiae. Exempli gratia, S={a,{a}}{displaystyle S={a,{a}}} est copia cuius elementa sunt a et copia alia {a} (cuius elementum est ipsa a). Numerus elementorum copiae nomine cardinalitatis vel magnitudine copiae appellatur, sive finita sive infinita. Sit S = {a, b, c}; tum cardinalitas copiae S est 3.[2]
Si S, T sunt copiae, et omnia elementa S sunt elementa etiam T, copia S dicitur copia inferior copiae alterius, quae ea de re copia superior appellatur. Hoc est, si S={a,c,e},T={a,b,c,d,e,f},{displaystyle S={a,c,e},T={a,b,c,d,e,f},} tum S⊂T{displaystyle Ssubset T} et T⊃S{displaystyle Tsupset S}. Copia vacua est copia inferior omnium aliarum copiarum. Omnis copia est inferior sui ipsius (hoc est, semper S⊂S{displaystyle Ssubset S}), sed copiae inferiores proprie dictae sunt copiae inferiores quae suas copias superiores non aequant. Si S et T sunt copiae, fieri potest ut non sit nec S⊂T{displaystyle Ssubset T} nec T⊂S{displaystyle Tsubset S}: exempli gratia, si S={a,1,b,2}{displaystyle S={a,1,b,2}} et T=a,b,c,d{displaystyle T={a,b,c,d}}, tum nec S⊂T{displaystyle Ssubset T} quod 1∈S,1∉T{displaystyle 1in S,1notin T}, nec T⊂S{displaystyle Tsubset S}, quod d∈T,d∉S{displaystyle din T,dnotin S}.
Duae copiae, quae eadem elementa habent, sunt eadem copia, etiamsi elementa varie scribuntur. Exempli gratia, sit S = {1, 2, 3, 4, 5} et T = {5, 4, 3, 2, 1}; tum S = T. Copia vacua est solum una.
Copia infinita est si ei tantundem elementorum est, quantum habet copia sua inferior proprie dicta. Duo copiae inter se numero elementorum (i. e. cardinalitate) aequales sunt, si est functio biiectiva quae omni elemento unius copiae elementum alterius copiae attribuit. Exempli gratia, copiae {a, b, c} et {1, 2, 3} eiusdem cardinalitatis sunt, quod functio elementa (a, 1), (b, 2), (c, 3) attribuit. Sed {a, b, c} est copia finita, quod copiae eius inferiores pauciora elementa habent. Copia autem numerorum naturalium est copia infinita: functio f(x) = 2x omni numero naturali unum numerum parem aggregat, et rursum omni numero pari y unum numerum naturalem y/2. Numeri pares hic sunt copia inferior, quia numerus par semper est numerus naturalis, et copia inferior proprie dicta, quia copiae numerorum naturalium etiam numeri impares sunt. Atqui eo quod tantundem numerorum naturalium est quantum numerorum parium, hae duae copiae infinitae sunt.
Copiae infinitiae sunt aut numerabiles aut innumerabiles. Copia est numerabilis si eandem cardinalitatem habet atque copia numerorum naturalium; copiae finitae quoque numerabiles dicuntur. Copia innumerabilis maior est quam copia numerabilis, hoc est, maiorem cardinalitatem habet. Exempli gratia, copia numerorum realium est innumerabilis, ut Cantor demonstravit.[3]
Operationes |
Copia cuius elementa sunt copiae inferiores cuiusdam copiae dicitur copia potens vel potentiae huius copia, aut copia partium.[4] Copia potens cuiusdam copiae semper plura elementa habet quam haec copia ipsa. Exempli gratia, sit S = {a, b, c}. Tum copia potens S, vel P(S){displaystyle {mathcal {P}}(S)}, 8 elementa habet:
- P(S)={∅,{a},{b},{c},{a,b},{a,c},{b,c},S}{displaystyle {mathcal {P}}(S)={emptyset ,{a},{b},{c},{a,b},{a,c},{b,c},S}}
Si S est copia finita et n elementa habet, cardinalitas copiae potentis S est 2n. Si S est copia infinita cuius cardinalitas est α, 2α significat cardinalitas copiae potentis S, per definitionem.
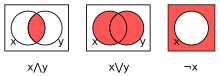
Diagrammata Venniana quae monstrant operationes intersectionis, unionis complementique vel negationis
Coniunctione aut unione duarum copiarum fit nova copia, quae omnia elementa harum duarum copiarum habet. Exempli gratia, sint S = {a, b, c} et T = {1, 3, 5}. Tum S∪T=a,b,c,1,3,5{displaystyle Scup T={a,b,c,1,3,5}}.
Aut, si S = {a, b, c} et T = {c, d, e}, tum S∪T=a,b,c,d,e{displaystyle Scup T={a,b,c,d,e}}; elementum c, etiamsi est elementum ambarum copiarum, modo semel reperitur inter elementa novae copiae.
Intersectio duarum copiarum est nova copia, cuius elementa sunt omnia elementa quae in ambabus copiis insunt. Exempli gratia, si S = {a, b, c, d, e} et T = {a, c, e, g, i}, tum S∩T=a,c,e{displaystyle Scap T={a,c,e}}.
Aut, si S = {a, b, c} et T = {1, 3, 5}, tum S∩T=∅{displaystyle Scap T=emptyset }.
Differentia copiae S e copia T est nova copia, cuius elementa sunt omnia elementa quae in S insunt, sed in T non insunt. Hoc est, si S = {a, b, c, d, e, f, g, h, i} et T = {f, g, h, i}, tum S∖T=a,b,c,d,e{displaystyle Ssetminus T={a,b,c,d,e}}.
Complementum copiae S in universa U est nova copia, cuius elementa sunt omnia elementa universae quae non in S insunt. Exempli gratia, si universa est copia numerorum naturalium, et si S est copia numerorum naturalium parium, tum ¬S{displaystyle neg S} est copia numerorum naturalium imparium. Non est complementum sine universa data.
Universa est copia quae continet omnia elementa omnium copiarum de quibus tractamus. Exempli gratia, si analysin realem facimus, universa est R{displaystyle mathbb {R} }, numeri reales. Sed si de theoria numerorum agitur, fortasse universa est Z{displaystyle mathbb {Z} }, numeri integri. Scilicet non necesse est elementa esse numeros.
Axiomata et problemata |
Copiae mathematicae ante quam data sunt axiomata formalia collectiones esse quarumvis rerum, dum definitio daretur, receptae sunt. Russell verum cum Zermelo paradoxon dedit, quo monstratum est copiam non esse quamvis aliqua definitione determinatam, perque consequentiam theoriam simplicem sibi congruere redarguit. Axiomata Zermelo-Fraenkel igitur prodita sunt, per quae vetantur eiusmodi copiae, ut theoria sibi congruere speretur.
Sunt autem multa problemata amplissima e theoria copiarum orta, quorum praecipuum et notissimum est hypothesis continui vel saepius CH, quae nullam copiam esse maiorem quam copiam numerorum integrorum, minorem quam copiam numerorum realium vult, aut notis cardinalium 2ω=ω1{displaystyle 2^{omega }=omega _{1}}. Hypothesis est quoque continui expansa vel GCH, quae 2κ=κ+{displaystyle 2^{kappa }=kappa ^{+}} omnibus cardinalibus κ{displaystyle kappa } vult.
Disciplina theoriae |
Exemplaria interiora |

Hypothesis continui: quid est cardinalitas P(N){displaystyle {mathcal {P}}(mathbb {N} )}?
Copiae rite ab imo structae quia diversas theorias mathematicae aemulari possunt, a David Hilbert et aliis pro fundamento huius doctrinae sumptae et nobis eis finibus traditae sunt. Nonne verum comprobare fundamentum mathematicum sibi congruere volumus, ne quid antinomiae comprobet? Profecto nequimus: anno 1931 a Kurt Gödel edita sunt theoremata de imperfectione, quae nos nullam probationem congruentiae axiomatum quorumvis per ipsa dare posse monstravit, nisi haec axiomata sibi non congruunt. Ut exemplo est, si Con(ZFC) congruentiam axiomatum ZFC signat, tum
- ZFC⊬Con(ZFC){displaystyle mathrm {ZFC} nvdash operatorname {Con} (mathrm {ZFC} )}
Nihilominus, si Con(ZFC) asciscimus atque per consequentiam exemplari eorum utimur, exemplaria aliorum axiomatum intus inveniri possunt. Pars exemplaris aliqui primigeni exemplar interius appellatur, si et ZF axiomata satisfacit et omnes cardinales exemplaris primigeni continet. Primum exemplar huius generis Gödel anno 1938 prodidit, nomine L{displaystyle L} (mundus constructibilis): exemplar non solum axiomatum ZFC est ab exemplar ZF definitum, sed etiam hypothesin continui expansam satisfacit, quare comprobavit
- Con(ZF)⊢Con(ZFC+GCH){displaystyle operatorname {Con} (mathrm {ZF} )vdash operatorname {Con} (mathrm {ZFC+GCH} )}
Axiom V=L igitur omne exemplar primigenum in L inesse vult.
Modus coercens |
Exemplari ZFC posito fortasse Con(¬GCH) comprobare volumus aut Con(¬AC), id est axioma electionis, cuius per consequentiam GCH et AC non in ZF pendere videamus. Quid agamus? Certe nullum erit exemplar interius quod ¬GCH aut ¬AC satisfaciat, quia si V=L in exemplar primigenum, tum nullum est exemplar interius nisi quod iam habemus.
Anno 1963 praeclarissimus modus coercens (anglice "forcing") a Paul Cohen inventus est ad resolvendum hoc problema, quo modo functiones in exemplari addi possunt, ut cardinalitas 2ω{displaystyle 2^{omega }} mutetur et aequa ac, ut exemplo est, ω2{displaystyle omega _{2}} sit, nec minus axiomata ZFC satisfaciantur. Porro autem W. B. Easton modum excoluit ut cardinalitas copiarum partium cardinalium omnino libere mutari possint, nisi leges simplices (incrementum continuum, theorema Cantor, theorema König) contradictentur.
Cardinales permagni |
Cardinales permagni sunt eiusmodi numeri cardinales infiniti, qui ob suam immanitatem plus praebeant facultatis monstrandi.
Ut exemplo est, cardinalis regularis κ{displaystyle kappa } eiusmodi sumamus, ut 2<κ<κ{displaystyle 2^{<kappa }<kappa }. Hic cardinalis "inaccessus" appellatur, quod nullo modo accedi potest a minoribus cardinalis (nec supremo concipiendo nec copia partium), porro enim monstrari potest Vκ{displaystyle V_{kappa }} esse exemplar axiomatum ZF. Suntne verum cardinales inaccessi? In axiomatibus ZF non pendet hoc problema: alia sunt exemplaria quae cardinales inaccessos contineant, alia sunt in quibus nulli sint hi cardinales.
Sit T theoria formalis extendens ZF+DC (id est axioma electionis consequentis) quae "omnes copias numerorum realium metro Lebesgue metiri posse" vult. Monstratum est a Shelah (1984) nec Con(T) nec ¬Con(T) a Con(ZFC) sequi, etsi Solovay (1970) iam Con(T) a Con(ZFC+"est cardinalis inaccessus") consequi monstravit, quippe igitur cardinales inaccessi plus facultatis monstrandi praebent.
Historia |
Georgius Cantor theoriam copiarum anno 1874 primus definit, in articulo qui inscribitur Über eine Eigenschaft des Inbegriffs aller reelen algebraischen Zahlen, hoc est Latine De proprietate copiae omnium numerorum algebraicorum realium. Hoc in articulo demonstravit copiam numerorum realium maiorem esse quam copiam numerorum rationalium: id est, infinitas non una res est, nec una quantitas, sed plures.
Ernestus Zermelo axiomata anno 1908 formulavit.
Nexus interni
- Supremum
- Topologia
Notae |
↑ Enderton 1972:4, hanc theoriam nominat "ordinaria et cottidiana utilia theoriae copiarum" (Anglice "normal everyday set-theoretic apparatus").
↑ Hae definitiones et sequentes facile explicantur ab Enderton 1972:4-13.
↑ Jech, p. 37, demonstrationem explicat.
↑ Francogallice ensemble des parties, hispanice conjunto potencia
Bibliographia |
- Aczel, Peter. 1988. Non-well-founded Sets. CSLI Lecture Notes, 14. Stanford. ISBN 0-937073-21-0.
- Bandmann, Hans. 1992. Die Unendlichkeit des Seins: Cantors transfinite Mengenlehre und ihre metaphysichen Wurzeln. Peter Lang. ISBN 3-631-42559-7.
- Barwise, Jon, ed. 1977. Handbook of Mathematical Logic. North-Holland. ISBN 0-7204-2285-X.
- Bourbaki, Nicolas. 1970. Théorie des ensembles. Hermann; re-ed Springer 2006. ISBN 978-3-540-34034-8.
Cantor, Georg. 1932 Gesammelte Abhandlungen mathematischen und philosophischen Inhalts. re-editio 1980, Springer.- Cohen, Paul J. 1963-1964. "The Independence of the Continuum Hypothesis." Proc. Nat. Acad. Sci. USA 50 (1963), 1143-1148, 51 (1964), 105-110.
- Cohen, Paul. J. 1966. Set Theory and the Continuum Hypothesis. Benjamin; re-editio Dover, 2008. ISBN 978-0-486-46921-8.
Dedekind, Richard. 1872. Stetigkeit und irrationale Zahlen. F. Vieweg und Sohn.- Devlin, Keith. 1993. The Joy of Sets. Ed. 2a. Springer Verlag. ISBN 0-387-94094-4.
- Enderton, Herbert B. 1972. A Mathematical Introduction to Logic. Academic Press.
- Ferreirós, Jose. (1999) 2007. Labyrinth of Thought: A history of set theory and its role in modern mathematics. Basel: Birkhäuser. ISBN 978-3-7643-8349-7.
- Foreman, Matthew, et Akihiro Kanamori, eds. 2010. Handbook of Set Theory. 3 voll.
- Fraenkel, Adolf. 1928, 1972. Einleitung in die Mengenlehre. Ed. 2a. Walluf: Martin Sändig oHG. ISBN 3500249604. Prima editio Berolini, Heidelberg, Novi Eboraci: Springer Verlag.
- Hausdorff, Felix. 1927. Mengenlehre. De Gruyter. OCLC 997955.
- Jech, Thomas. 1973. The Axiom of Choice. North-Holland. ISBN 0-444-10484-4.
- Jech, Thomas. 2003. Set Theory, editio tertia. Springer. ISBN 3-540-44085-2.
- Johnson, Philip. 1972. A History of Set Theory. Prindle, Weber & Schmidt. ISBN 0-87150-154-6.
- Kunen, Kenneth. 1980. Set Theory: An Introduction to Independence Proofs. North-Holland. ISBN 0-444-85401-0.
- Mayberry, J. P. 2000. The Foundations of Mathematics in the Theory of Sets. Cambridge. ISBN 0-521-77034-3.
- Machover, Moshé. 1996. Set Theory, Logic, and their Limitations. Cambridge. ISBN 0-521-47998-3.
- Suppes, Patrick. 1960. Axiomatic Set Theory. D. Van Nostrand; reeditio Dover, 1972. ISBN 0-486-61630-4.
- Tiles, Mary. (1989) 2004. The Philosophy of Set Theory: An Historical Introduction to Cantor's Paradise. Dover Publications.
Nexus externi |
Vicimedia Communia plura habent quae ad theoriam copiarum spectant. |
Paginae mathematicorum qui theoriam copiarum colunt
Theoria copiarum, pagina in encyclopedia philosophiae Stanfordense .mw-parser-output .existinglinksgray a,.mw-parser-output .existinglinksgray a:visited{color:gray}.mw-parser-output .existinglinksgray a.new{color:#ba0000}.mw-parser-output .existinglinksgray a.new:visited{color:#a55858}
(Anglice)
Theoria copiarum et fundamenta mathematicae, pagina Francogallice scripta a Sylvano Poirier
Theoria copiarum apud Sciences.ch
(Francogallice)
Theoria copiarum apud Universitatem Lugdunensem
(Francogallice)
Libri et articuli de theoria copiarum, logica mathematica, et aliis partibus mathematicae, a Carolo Ivorra scripti
(Hispanice)

































